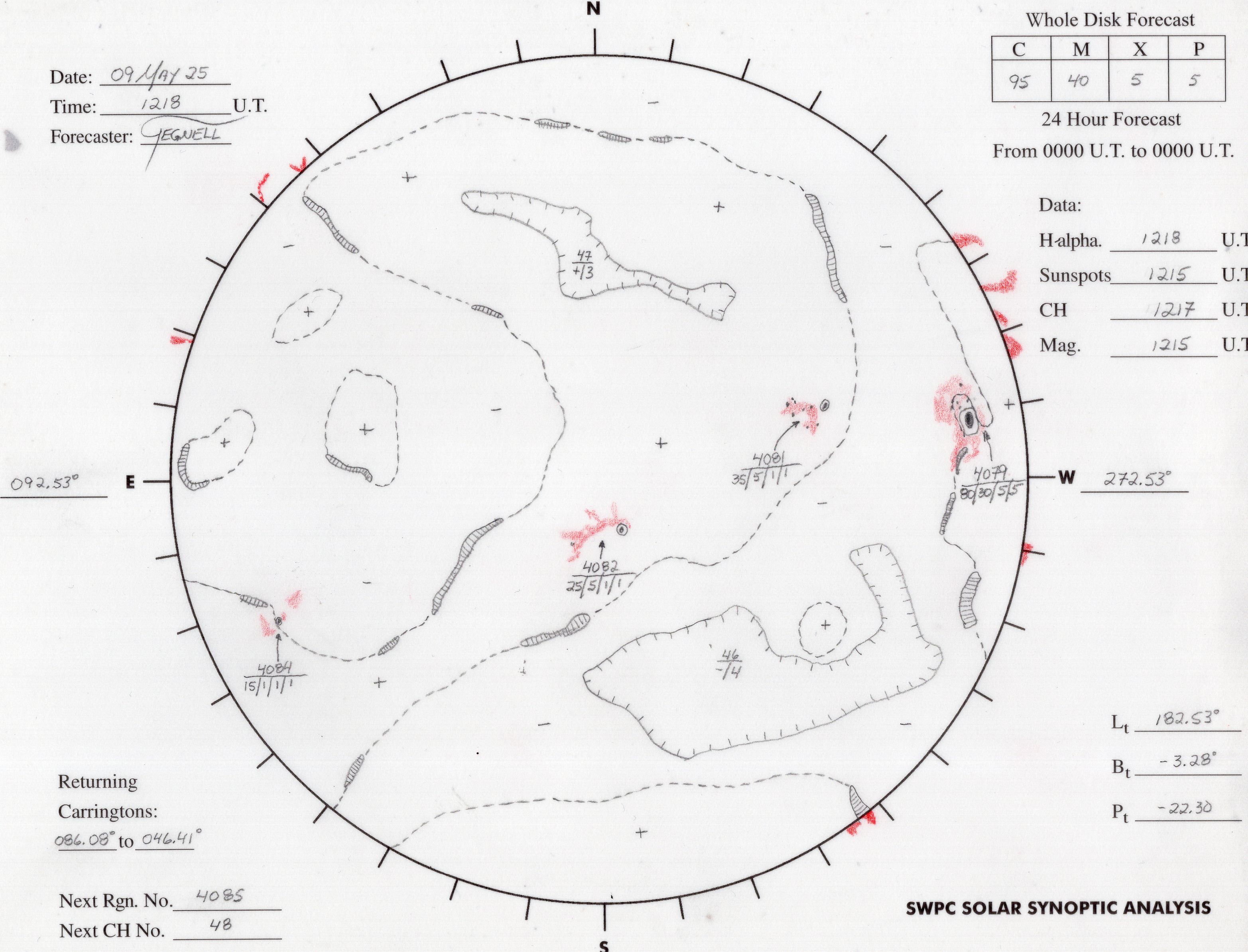
El problema de rastrear la trayectoria de una nave espacial Apolo.

Rastrear la nave espacial Apolo fue un desafío para los científicos de la NASA. Crédito: NASA
Cuando la NASA decidió por primera vez poner a un hombre en la Luna, tuvieron un problema. En realidad, tuvieron varios problemas. Era la primavera de 1960, y no solo no habían enviado a un hombre al espacio, sino que la Unión Soviética había ganado recientemente la carrera para poner un satélite en órbita. Luego estaban los problemas técnicos: las tuercas y los pernos de cómo transportar a tres hombres a 238,900 millas desde un sitio de lanzamiento en Florida a la Luna, y de nuevo, todo antes de que los soviéticos los golpearan.
Uno de los obstáculos más grandes fue estimar la trayectoria de la nave: ¿cómo podría la NASA enviar astronautas a la Luna si no supieran dónde estaban? Los investigadores de la División de Análisis Dinámicos de la NASA en California ya habían estado trabajando en el problema durante varios meses, con un éxito limitado. Afortunadamente para el programa Apollo que estaba a punto de cambiar.
Aleatoriedad y errores
El trabajo de las trayectorias había resultado difícil para los investigadores porque realmente estaban tratando de resolver dos problemas a la vez. La primera fue que las naves espaciales no se aceleran y se mueven sin problemas en la vida real, como lo harían en un libro de texto de física. Están sujetos a efectos variables como la gravedad lunar, que a menudo son desconocidos. Esta aleatoriedad significaba que incluso si los científicos hubieran observado la posición exacta de la nave, la trayectoria no seguiría un camino limpio y predecible.
Pero ese era su segundo problema: no podían observar su posición exacta. Aunque los sensores a bordo incluían un sextante, que calculaba el ángulo de la Tierra y la Luna en relación con la nave espacial y los giroscopios, no estaba claro cómo estos datos, que inevitablemente contenían errores de medición, podrían traducirse con precisión a la posición y la velocidad.
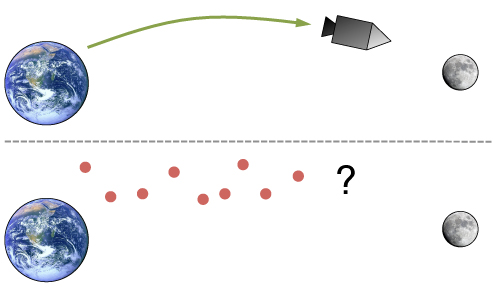
Arriba: En un mundo perfecto, la nave tendría una trayectoria simple “de libros de texto”.
Parte inferior: en realidad, su movimiento está sujeto a aleatoriedad, al igual que las medidas utilizadas para estimar su posición (desconocida).
Stanley Schmidt, el ingeniero que dirigió la División de Análisis Dinámico, inicialmente esperaba utilizar ideas desarrolladas para misiles de largo alcance, otro producto de la rivalidad de la Guerra Fría con la Unión Soviética. Sin embargo, los sistemas de navegación con misiles tomaron medidas casi continuamente, mientras que durante una misión ocupada, la nave Apollo solo podría tomarlos a intervalos irregulares. Schmidt y sus colegas pronto se dieron cuenta de que los métodos existentes no podrían darles estimaciones lo suficientemente precisas: necesitaban encontrar un nuevo enfoque.
Lo que sucedió después fue un increíble golpe de buena suerte. En el otoño de 1960, un viejo conocido de Schmidt, que no tenía idea del trabajo que estaban realizando los científicos de la NASA, llamó para concertar una visita. Rudolph Kalman era un matemático con sede en Baltimore, y quería venir y discutir su última investigación.
El filtro de Kalman.
Kalman se especializó en ingeniería eléctrica y recientemente encontró una forma de convertir una serie de mediciones no confiables en una estimación de lo que realmente estaba sucediendo. Sin embargo, sus resultados matemáticos fueron recibidos con escepticismo, y Kalman aún tenía que encontrar una manera de convertir su teoría en una solución práctica.
Schmidt no necesitaba ser convencido. Después de escuchar la presentación de Kalman, distribuyó copias del método a los ingenieros de la NASA y trabajó con Kalman para desarrollar una forma de aplicarlo a su problema. A principios de 1961 tenían su solución.
La técnica de Kalman se llamó filtro y se trabajó en dos pasos. El primero utilizó la física newtoniana para hacer una predicción sobre el estado actual del sistema (en el caso de la NASA, la ubicación de la nave espacial) y el nivel de incertidumbre debido a los posibles efectos aleatorios. El segundo paso luego utilizó un promedio ponderado para combinar la medición observada más recientemente, que inevitablemente tuvo algún grado de error, con esta predicción.
Para un ejemplo simplificado, supongamos que una mini nave se mueve a lo largo del borde de una regla entre los números 0 y 1. Suponga que la posición predicha en un momento dado es y la posición observada es . Si representa el nivel relativo de confianza en la predicción en comparación con la observación, el promedio ponderado es

Si tenemos la misma confianza en la precisión de las posiciones pronosticadas y observadas, podríamos asumir que el promedio ponderado sería un promedio simple de los dos valores
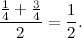
Pero el filtro de Kalman hace algo más inteligente que esto. Toma el nivel de aleatoriedad que entró en la predicción y la cantidad de error que creemos que hay en la medición, y los combina para proporcionar el valor óptimo para la confianza relativa . Si se confió más en la predicción que en la medición, se otorga más peso a la predicción. A la inversa, si las mediciones eran más plausibles, entonces se les da más preferencia.
Un ejemplo de un promedio ponderado que otorga más peso a la posición predicha que la observada (de hecho, el doble de peso) sería uno donde, en este caso, el filtro nos da una estimación más cercana a la posición predicha.
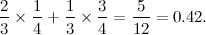
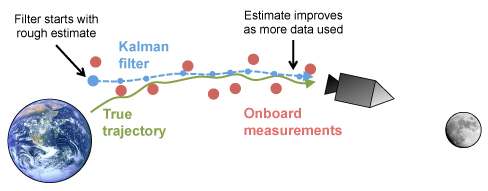
El filtro de Kalman compara las predicciones utilizando las Leyes de Newton con las mediciones a bordo para generar una mejor estimación de la verdadera posición de la nave.
Además de producir estimaciones precisas, el filtro de Kalman podría ejecutarse en tiempo real: todo lo que necesitaba para generar una estimación era la predicción previa y la medición actual a bordo. Debido a que cualquier cálculo tendría que hacerse en la primitiva computadora a bordo del Apollo, esta simplicidad hizo que el filtro fuera increíblemente valioso. De hecho, eventualmente se usaría en los seis aterrizajes de la Luna, así como para encontrar su camino en los sistemas de navegación de submarinos nucleares, aviones y la Estación Espacial Internacional.
De las trayectorias a la transmisión de enfermedades.
Décadas después de los desembarcos de la Luna aún quedan preguntas sobre la mejor forma de estimar la información oculta, y no son solo los ingenieros los que les preguntan. Los investigadores de enfermedades se han preguntado durante mucho tiempo cómo entender la verdadera propagación de una infección (que no pueden ver) mediante informes de casos de hospitales (que pueden). En cierto modo, no es tan diferente del problema que tenía la NASA. Incluso si los investigadores intentan y hacen predicciones asumiendo que una enfermedad se transmite de cierta manera, su propagación todavía se verá afectada por la aleatoriedad. Y es poco probable que la proporción de personas infectadas que acuden a ver a un médico permanezca constante, lo que significa que cualquier método de medición, por ejemplo, suponiendo que los informes hospitalarios representan una cierta fracción del total de infecciones, también está sujeto a errores.
Soluciones modernas a un problema histórico.
Años después de que finalizó el programa Apollo, Stanley Schmidt y uno de sus colegas produjeron un informe que documenta su trabajo sobre las predicciones de la trayectoria. Como era de esperar, tuvieron muchos elogios para el filtro de Kalman. “La amplia aplicación del filtro a problemas aparentemente improbables sugiere que solo hemos arañado la superficie cuando se trata de posibles aplicaciones”, escribieron, “y que es probable que nos sorprendamos con las aplicaciones a las que se le aplicará este filtro en los próximos años.”
Resultó ser una predicción astuta. Los investigadores de enfermedades ahora emplean filtros para determinar qué causa los brotes. Los científicos de la atmósfera los utilizan para dar sentido a los patrones climáticos. Los economistas aplican los métodos a los datos financieros. Las técnicas pueden haber comenzado como una forma de guiar a tres hombres a la Luna, pero desde entonces se han convertido en un valioso conjunto de herramientas para abordar los problemas aquí en la Tierra.
Fuente: +Plus Magazine/University of Cambridge.
Artículo original: “Understanding the unseen“. Dr. Adam Kucharsky.
Nota del editor: Para no dilatar la extensión de la publicación he omitido la publicación de una parte del artículo, que trata sobre la aplicación del filtro de Kalman a investigaciones de propagación de infecciones, que si el lector lo desea, puede leerlo en el artículo original.
Material relacionado:
Una relato de esta historia se encuentra en el siguiente artículo:
Stanley Schmidt Former NASA Ames Aerospace Engineer Dies. NASA/Ames Research Center.October 25, 2015.
El siguiente artículo ilustra cómo era el campo gravitatorio de la Luna supuesto en los cálculos de la trayectoria y cuál es el real con el que tuvo que lidiar la misión:
How complex was the math and physics necessary to place Apollo 11 on the moon?. Space Exploration Stack Exchange . Dec. 3, 2017.